657 Thousand Times 1 Thousand
rt-students
Sep 10, 2025 · 6 min read
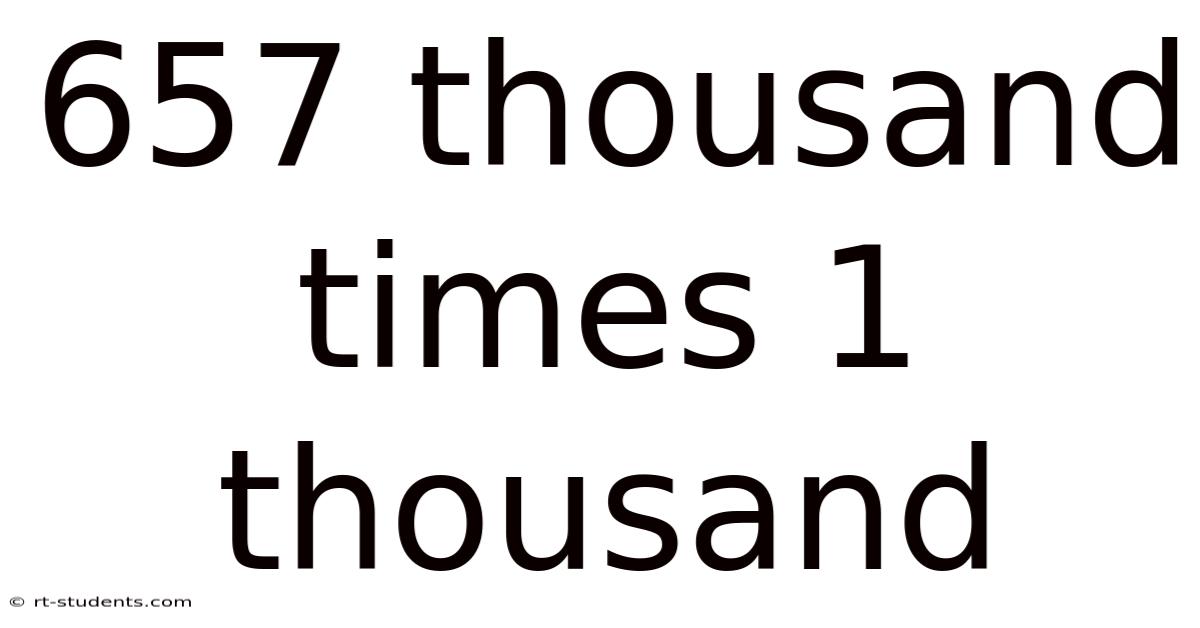
Table of Contents
Decoding the Calculation: 657 Thousand Times 1 Thousand
This article delves into the seemingly simple yet conceptually significant calculation of 657 thousand multiplied by 1 thousand. While the arithmetic is straightforward, understanding the underlying principles and exploring the implications of such large numbers provides a valuable learning experience in mathematics, particularly in scaling and working with large datasets. We'll cover the basic calculation, explore the significance of the result, and discuss real-world applications. This will help solidify your understanding of large number manipulation and its relevance in various fields.
Understanding the Fundamentals: Multiplication of Large Numbers
At its core, this problem involves multiplying 657,000 by 1,000. This is a fundamental mathematical operation that forms the basis for many advanced calculations. Let's break it down step-by-step:
-
The Basics of Multiplication: Multiplication is essentially repeated addition. Multiplying 657,000 by 1,000 means adding 657,000 to itself 1,000 times. However, performing this directly is incredibly inefficient.
-
Using Place Value: Understanding place value is crucial when dealing with large numbers. In the number 657,000, each digit represents a specific power of 10:
- 6 represents 6 hundred thousands (600,000)
- 5 represents 5 ten thousands (50,000)
- 7 represents 7 thousands (7,000)
- 0 represents 0 hundreds (0)
- 0 represents 0 tens (0)
- 0 represents 0 ones (0)
-
Multiplying by Powers of 10: Multiplying a number by 1,000 (which is 10³) is a particularly simple operation. It's equivalent to shifting the decimal point three places to the right. Since we're dealing with whole numbers, this means adding three zeros to the end of the number.
Performing the Calculation: 657,000 x 1,000
Using the shortcut method of multiplying by a power of 10, the calculation becomes trivial:
657,000 x 1,000 = 657,000,000
Therefore, 657 thousand times 1 thousand equals 657 million.
The Significance of the Result: Exploring Scale and Magnitude
The result, 657,000,000, represents a significant quantity. The sheer magnitude of this number helps illustrate the power of exponential growth and the scale at which certain phenomena occur. Consider these points:
-
Visualizing the Number: It's difficult to truly grasp the size of 657 million. Imagine trying to count that many grains of sand, or stars in the sky. The number surpasses the population of many countries and highlights the scale of certain global issues.
-
Exponential Growth: This calculation is a simple example of exponential growth. If we were to consider a scenario where a quantity increases by a factor of 1,000, the implications become clear – starting with a relatively small number can lead to an enormous result in just a few iterations.
-
Applications in Various Fields: Understanding the manipulation of large numbers like this is crucial in diverse fields such as:
- Finance: Dealing with large sums of money, investments, and national budgets.
- Science: Analyzing large datasets, modeling complex systems, and understanding astronomical scales.
- Engineering: Designing infrastructure, managing resources, and calculating material quantities.
- Data Science: Processing and interpreting large datasets, building predictive models, and drawing meaningful conclusions.
Real-World Applications and Examples
Let's look at some real-world scenarios where a similar calculation might arise:
-
Population Growth: Imagine a city with a population of 657,000. If the population were to increase by a factor of 1,000 (perhaps due to rapid urbanization and immigration over a long period), the resulting population would be 657 million.
-
Resource Management: Consider a nation's annual energy consumption. If a country consumes 657,000 units of energy per day, its total consumption over 1,000 days (approximately 3 years) would be 657 million units.
-
Data Analysis: Imagine a database containing 657,000 entries. If each entry requires 1,000 bytes of storage space, then the total storage requirement would be 657 million bytes (or 657 MB).
-
Financial Investments: If an investment yields a return of 657,000 units per year, and this trend continues for 1,000 years (a highly theoretical example), the total yield would be 657 million units.
Expanding the Concept: Beyond Simple Multiplication
While the calculation itself is basic, the principles involved have broader applications. Here are some related concepts to consider:
-
Scientific Notation: For very large numbers, scientific notation is a more compact and convenient way to represent them. 657,000,000 could be written as 6.57 x 10⁸. This method simplifies calculations and comparisons of extremely large or small numbers.
-
Orders of Magnitude: Understanding orders of magnitude helps compare the relative sizes of different numbers. The difference between 657,000 and 657,000,000 is several orders of magnitude – a significant disparity.
-
Significant Figures: In scientific and engineering calculations, the number of significant figures is important to indicate the precision of a measurement or calculation.
-
Rounding and Estimation: For many purposes, it's sufficient to round large numbers to simplify calculations and estimations.
Frequently Asked Questions (FAQ)
Q: What is the best way to calculate 657,000 x 1,000 quickly?
A: The easiest method is to add three zeros to the end of 657,000, resulting in 657,000,000. This is because multiplying by 1,000 (10³) is equivalent to shifting the decimal point three places to the right.
Q: Are there any other methods to solve this problem?
A: Yes, you could use long multiplication, but it's far less efficient for this specific problem. Long multiplication would involve multiplying each digit of 657,000 by each digit of 1,000 and then adding the partial products. However, given the nature of multiplying by a power of 10, this approach is unnecessarily complex.
Q: What are the practical applications of understanding this type of calculation?
A: Understanding large-number calculations like this is crucial in various fields including finance, science, engineering, and data science. It helps in managing large datasets, resource allocation, financial modeling, and scientific simulations.
Q: How can I improve my skills in handling large numbers?
A: Practice is key. Work through various problems involving multiplication and division of large numbers. Familiarize yourself with scientific notation and orders of magnitude. Use online calculators and resources to check your answers and gain experience.
Conclusion: Mastering Large Numbers, Mastering Concepts
This article demonstrated the calculation of 657 thousand multiplied by 1 thousand, resulting in 657 million. While the arithmetic was straightforward, the real value lies in understanding the implications of working with large numbers, their relevance in various fields, and the associated mathematical concepts. This understanding is crucial for anyone working with data, finances, or any field involving significant quantities. Mastering the manipulation of large numbers is not just about performing calculations; it's about developing a deeper understanding of scale, magnitude, and the power of exponential growth. By applying the principles discussed here, you'll be better equipped to tackle complex mathematical problems and understand the world around you on a larger scale.
Latest Posts
Latest Posts
-
Stages Of The Policymaking Process
Sep 10, 2025
-
Which Shot Hurts The Most
Sep 10, 2025
-
General Survey For Health Assessment
Sep 10, 2025
-
Does Simple Diffusion Require Energy
Sep 10, 2025
-
10 15 On A Clock
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about 657 Thousand Times 1 Thousand . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.