Fv Of Growing Annuity Formula
rt-students
Sep 13, 2025 · 6 min read
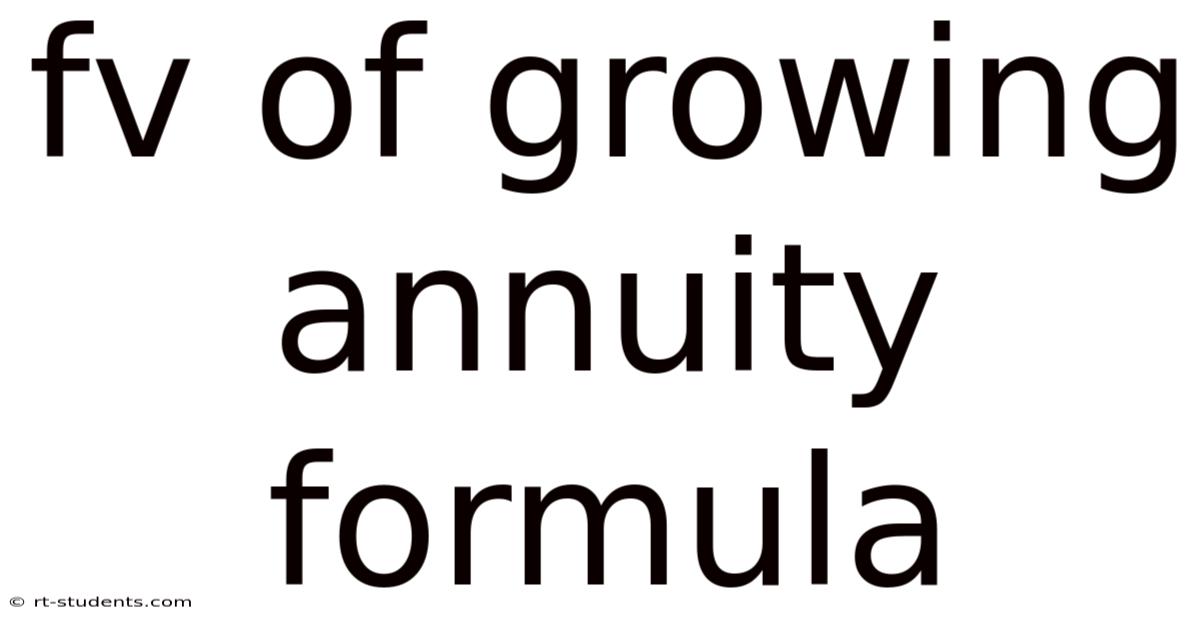
Table of Contents
Understanding the Future Value of a Growing Annuity: A Comprehensive Guide
The future value (FV) of a growing annuity is a crucial concept in finance, particularly for understanding investments and retirement planning. It calculates the future worth of a series of payments that increase at a constant rate over a specified period. This differs from a regular annuity where payments remain constant. This article provides a comprehensive explanation of the FV of a growing annuity formula, its applications, and the underlying principles. We will explore the formula itself, delve into its derivation, and provide practical examples to solidify your understanding.
What is a Growing Annuity?
A growing annuity is a stream of cash flows received or paid at regular intervals, where each subsequent payment is larger than the previous one by a fixed percentage. This percentage increase is often referred to as the growth rate. This contrasts with a regular annuity, where payments remain the same throughout the payment period. Examples of growing annuities include:
- Regular investments in a savings plan: If you invest a fixed amount each month, but increase the investment amount by a certain percentage yearly, you are essentially creating a growing annuity.
- Dividend payments from a growing company: Companies often increase their dividend payments over time as their earnings grow. This creates a growing annuity for shareholders.
- Salary increases over time: While not perfectly consistent, salary increases can often be modeled as a growing annuity for retirement planning purposes.
The Future Value of a Growing Annuity Formula
The formula for calculating the future value (FV) of a growing annuity is:
FV = P * [((1 + r)^n - (1 + g)^n) / (r - g)]
Where:
- FV = Future Value of the growing annuity
- P = Initial payment (the first payment in the series)
- r = Interest rate (or discount rate) per period. This is the rate at which your investments grow.
- g = Growth rate of the annuity per period. This is the rate at which your payments increase.
- n = Number of periods (e.g., number of years)
Important Considerations:
- Consistency of Rates: The interest rate (r) and the growth rate (g) must be expressed in the same terms as the number of periods (n). For example, if n is in years, r and g should also be annual rates.
- r > g: The formula is only valid if the interest rate (r) is greater than the growth rate (g). If g is greater than or equal to r, the denominator (r - g) becomes zero or negative, making the calculation impossible. This makes intuitive sense; if your payments grow faster than your investment earns, the future value will grow infinitely large.
Derivation of the Formula
The formula is derived using the concept of present value and the geometric series formula. Let's break down the derivation:
-
Present Value of Each Payment: Each payment in a growing annuity can be considered a single cash flow occurring at a specific time. To find the present value (PV) of each payment, we use the present value formula: PV = FV / (1 + r)^t, where 't' is the time period.
-
Geometric Series: The present values of the payments form a geometric series, where each term is multiplied by a common ratio (1 + g) / (1 + r).
-
Summation: We sum the present values of all payments in the series. This summation leads to a simplified expression that involves the geometric series formula.
-
Future Value: Finally, we multiply the sum of present values by (1 + r)^n to find the future value. This accounts for the compounding of interest over the entire period. The mathematical manipulation of the summation and the application of the geometric series formula results in the final formula stated above.
Practical Examples
Let's illustrate the formula with a few examples:
Example 1: Retirement Savings
Suppose you plan to invest $5,000 annually in a retirement account that earns an average annual return of 8% (r = 0.08). You plan to increase your annual investment by 3% (g = 0.03) each year for 20 years (n = 20). What will be the future value of your investment after 20 years?
Using the formula:
FV = 5000 * [((1 + 0.08)^20 - (1 + 0.03)^20) / (0.08 - 0.03)]
FV = 5000 * [(4.66096 - 1.80611) / 0.05]
FV = 5000 * [57.097]
FV ≈ $285,485
Therefore, after 20 years, your retirement savings will be approximately $285,485.
Example 2: Growing Dividends
Imagine you own stock in a company that pays an annual dividend of $10 per share. The company projects dividend growth of 4% per year (g = 0.04) for the next 10 years (n = 10). Assuming a discount rate of 7% (r = 0.07), what is the future value of the dividends over the next 10 years?
Using the formula:
FV = 10 * [((1 + 0.07)^10 - (1 + 0.04)^10) / (0.07 - 0.04)]
FV = 10 * [(1.96715 - 1.48024) / 0.03]
FV = 10 * [16.2303]
FV ≈ $162.30
The future value of the dividends over the next 10 years is approximately $162.30 per share.
Applications of the Growing Annuity Formula
The future value of a growing annuity formula finds applications in various financial scenarios:
- Retirement Planning: Predicting the future value of retirement savings, considering regular contributions that increase over time.
- Investment Analysis: Evaluating the future worth of investments that generate growing cash flows, such as dividend-paying stocks or real estate.
- Loan Amortization: Analyzing loan repayment schedules where payments increase over time, for example, in certain types of mortgages or student loans.
- Capital Budgeting: Evaluating the profitability of projects that generate growing cash flows over their lifespan.
Frequently Asked Questions (FAQ)
Q: What happens if the growth rate (g) is greater than the interest rate (r)?
A: The formula is invalid if g ≥ r. The denominator (r - g) would be zero or negative, resulting in an undefined or negative future value, which is not financially realistic. This implies that the payments are growing faster than the investment is earning, leading to an infinitely large future value.
Q: Can this formula be used for decreasing annuities?
A: No, this formula specifically applies to growing annuities where payments increase over time. A separate formula is needed for decreasing annuities, which would involve a negative growth rate. However, the concept of a negative growth rate would have to be carefully analyzed in context; it likely represents a declining payment scheme.
Q: What if payments are made more frequently than annually (e.g., monthly or quarterly)?
A: You need to adjust the interest rate (r), growth rate (g), and number of periods (n) accordingly. If payments are made monthly, you would use the monthly interest rate and growth rate, and n would represent the number of months.
Conclusion
Understanding the future value of a growing annuity is crucial for effective financial planning and investment analysis. The formula provides a powerful tool for calculating the future worth of a series of increasing payments, allowing individuals and businesses to make informed decisions about savings, investments, and long-term financial goals. While the formula may seem complex at first, mastering it opens doors to a deeper understanding of compound growth and its significance in various financial contexts. By applying the formula correctly and considering the important caveats, you can accurately project future financial outcomes and make better decisions for your financial well-being. Remember that seeking professional financial advice is always recommended for complex financial situations.
Latest Posts
Latest Posts
-
The Combining Form Kyph O Means
Sep 13, 2025
-
Horizontal Analysis Of Income Statement
Sep 13, 2025
-
Whats The Poin Tof Mythology
Sep 13, 2025
-
Cost Function And Revenue Function
Sep 13, 2025
-
Does Facilitated Transport Require Energy
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about Fv Of Growing Annuity Formula . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.