Is 1/6 Smaller Than 1/4
rt-students
Sep 24, 2025 · 5 min read
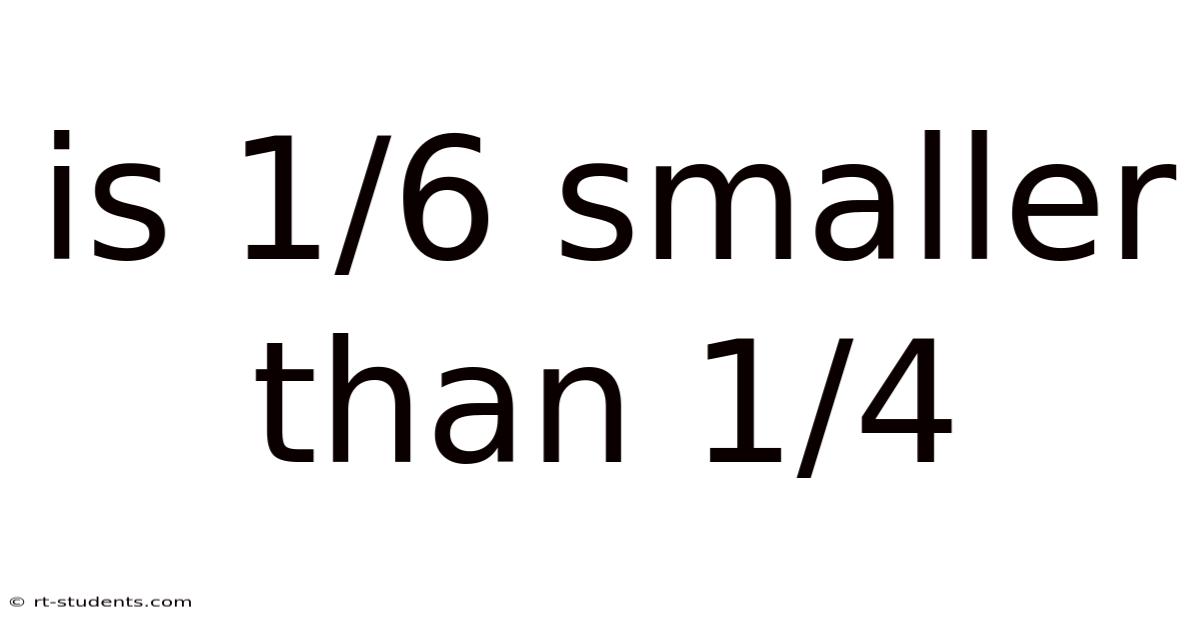
Table of Contents
Is 1/6 Smaller Than 1/4? A Deep Dive into Fraction Comparison
Understanding fractions is a fundamental concept in mathematics, crucial for various applications in everyday life and advanced studies. This article will comprehensively explore the question: "Is 1/6 smaller than 1/4?" We'll delve into multiple methods for comparing fractions, providing a clear and intuitive understanding for learners of all levels. We'll also explore the underlying principles and offer practical examples to solidify your comprehension.
Introduction: Understanding Fractions
Before directly comparing 1/6 and 1/4, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's written as a/b, where 'a' is the numerator (the number of parts we have) and 'b' is the denominator (the total number of equal parts the whole is divided into).
For instance, 1/4 represents one part out of four equal parts of a whole. Similarly, 1/6 represents one part out of six equal parts. The larger the denominator, the smaller each individual part becomes. This is the key to understanding the relative sizes of fractions.
Method 1: Visual Comparison using Diagrams
A simple and effective way to compare fractions is through visual representation. Imagine two identical pizzas.
- Pizza 1: Cut into four equal slices (representing 1/4).
- Pizza 2: Cut into six equal slices (representing 1/6).
Now, consider one slice from each pizza. You'll visually observe that the slice from Pizza 1 (1/4) is larger than the slice from Pizza 2 (1/6). This directly demonstrates that 1/6 is smaller than 1/4.
Method 2: Finding a Common Denominator
This is a more formal mathematical approach. To compare fractions, we need to express them with a common denominator – a shared bottom number. The least common multiple (LCM) of the denominators is the most efficient common denominator.
The denominators in our case are 4 and 6. Let's find their LCM:
- Multiples of 4: 4, 8, 12, 16, 20…
- Multiples of 6: 6, 12, 18, 24…
The least common multiple of 4 and 6 is 12.
Now, we convert both fractions to have a denominator of 12:
- 1/4 = (1 x 3) / (4 x 3) = 3/12
- 1/6 = (1 x 2) / (6 x 2) = 2/12
Now, comparing 3/12 and 2/12, it's evident that 3/12 (which is 1/4) is greater than 2/12 (which is 1/6). Therefore, 1/6 is smaller than 1/4.
Method 3: Decimal Conversion
Converting fractions to decimals provides another way to compare them. We can use a calculator or long division:
- 1/4 = 0.25
- 1/6 ≈ 0.1667
Since 0.25 > 0.1667, it confirms that 1/4 is larger than 1/6. This method is particularly useful when dealing with more complex fractions.
Method 4: Cross-Multiplication
This method is a shortcut for comparing fractions without finding a common denominator. We cross-multiply the numerators and denominators:
- 1/6 ? 1/4
- (1 x 4) ? (1 x 6)
- 4 ? 6
Since 4 < 6, it implies that 1/6 < 1/4. This method is efficient but requires careful attention to the direction of the inequality sign.
Illustrative Examples: Real-World Applications
Let's consider some real-world scenarios where comparing 1/6 and 1/4 is relevant:
- Sharing Pizza: If you have a pizza cut into six slices and another cut into four, a slice from the four-slice pizza is larger.
- Baking: If a recipe calls for 1/4 cup of sugar and you only have 1/6 cup, you will need more sugar.
- Measuring liquids: If you are measuring liquids and need 1/4 liter and only have 1/6 liter, you will need to add more liquid.
- Working on a project: If one task takes 1/4 of the total project time and another task takes 1/6 of the project time, the first task is longer.
Scientific Explanation: The Inverse Relationship between Denominator and Fraction Value
The core principle behind comparing fractions lies in the inverse relationship between the denominator and the value of the fraction. As the denominator increases (while the numerator remains constant), the value of the fraction decreases. This is because the whole is divided into more parts, making each individual part smaller.
Frequently Asked Questions (FAQ)
-
Q: Can we compare fractions with different numerators using the same methods?
- A: Yes, all the methods discussed (visual comparison, common denominator, decimal conversion, cross-multiplication) work equally well for comparing fractions with different numerators.
-
Q: What if the fractions are negative?
- A: The comparison principles remain the same. However, remember that negative fractions follow the opposite order of magnitude compared to positive fractions. For example, -1/6 is larger than -1/4 because it is closer to zero on the number line.
-
Q: Are there other methods to compare fractions?
- A: Yes, other advanced methods exist, especially for comparing complex fractions or dealing with multiple fractions simultaneously. These often involve simplifying fractions to their lowest terms or utilizing properties of inequalities.
-
Q: How can I improve my understanding of fraction comparison?
- A: Practice is key. Work through various examples, utilize different comparison methods, and check your answers. Visual aids and real-world applications can greatly enhance understanding.
Conclusion: Mastering Fraction Comparison
Comparing fractions is a fundamental skill in mathematics. Understanding the underlying principles, coupled with the ability to apply different comparison methods, enables accurate and efficient evaluation. Whether using visual aids, finding common denominators, decimal conversion, or cross-multiplication, the goal is to express the fractions in a way that allows for direct comparison of their magnitudes. Through practice and a clear understanding of these techniques, you can confidently tackle any fraction comparison problem. Remember, the larger the denominator, the smaller the fraction's value, provided the numerator stays the same. This simple rule forms the cornerstone of understanding fractional magnitudes.
Latest Posts
Latest Posts
-
Bible Map Of The World
Sep 24, 2025
-
Asam 3 5 Level Of Care
Sep 24, 2025
-
What Was Pantheon Used For
Sep 24, 2025
-
Words With The Stem Cent
Sep 24, 2025
-
Types Of Unemployment Ap Macro
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about Is 1/6 Smaller Than 1/4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.